因式分解公式法不会用,毫无疑问,乘法公式没掌握好,今天来学五大乘法公式及其变形。对于公式我们要知其也知其所以然,同时清楚的知道公式的相关变形。
先来看知识要点:
一、平方差公式
1.平方差公式:两个数的和与这两个数的差的乘积等于这两个数的平方差,即(a+b)(a-b)=a^2-b^2.
2.平方差公式变化(重要‼️)
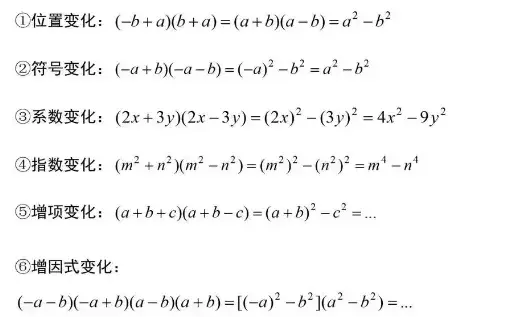
注意‼️公式中的字母,可以表示具体的数字,可以表示单项式,也可以表示多项式。
二、完全平方公式
1.完全平方公式:两数和(或差)的平方,等于它们的平方和,加上(或减去)它们积的两倍,即:(a+b)^2=a^2+2ab+b^2;(a-b)^2=a^2-2ab+b^2
注意‼️与平方差公式一样,公式中的字母可以代表一个数字,可以代表一个单项式,也可以是一个多项式。
2.完全平方公式的变形:
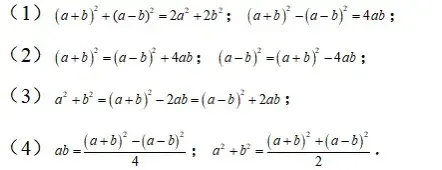
3.完全平方公式的应用推广:
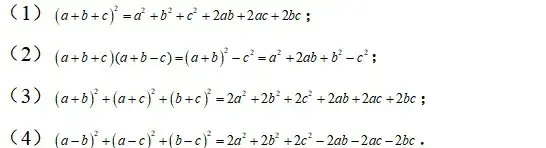
三、完全立方公式
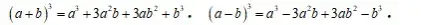
注意‼️杨辉三角与完全平方公式、完全立方公式的关系如下:

注:理解了杨辉三角与二次多项式的关系后,对于完全立方公式再也不会搞错了,对于一些拓展题也就明白了来龙去脉。
四、立方和、差公式
两数和(或差)乘以它们的平方和与积的差(或和),等于这两个数的立方和(或差), 这两个公式叫做乘法的立方和公式与立方差公式.即:
(a+b)(a^2-ab+b^2)=a^3+b^3
(a-b)(a^2+ab+b^2)=a^3-b^3

