曹冲生五六岁,智意所及,有若成人。时孙权尝致巨象,太祖欲知其斤重,访之群下,咸莫能出其理。冲曰:“置象于船上,而刻其水痕所至,称物以载之,则校可知矣。复称他物,则象重可知也”太祖悦,即施行焉。
上面这段文字你是否觉得很熟悉?
那时候的你学完这堂课后你学会了什么?
是否跟我一样只知道那时候的曹冲相对来说比较聪明。而没有去研究称象的这个方法所包含更深层的意义。最近忙完了一些事情,闲了下来。某天突然间想起这则故事,就多想了一下称大象的过程感觉还挺有趣的,接下来我们一起称大象吧。
把大象称一下需要几步?
曹冲的称大象过程
按照原文的步骤,第一步,置象于船上,而刻其水痕所至。把大象赶到船上,然后沿着水面在船体标记大象在船上时船体下沉的深度。
第二步,称物以载之,则校可知矣。把大象赶上岸后往船上装石头,使船体下沉到标注的位置。
第三步,复称他物,则象重可知也。使用称称出石头的重量,就知道大象的总量。
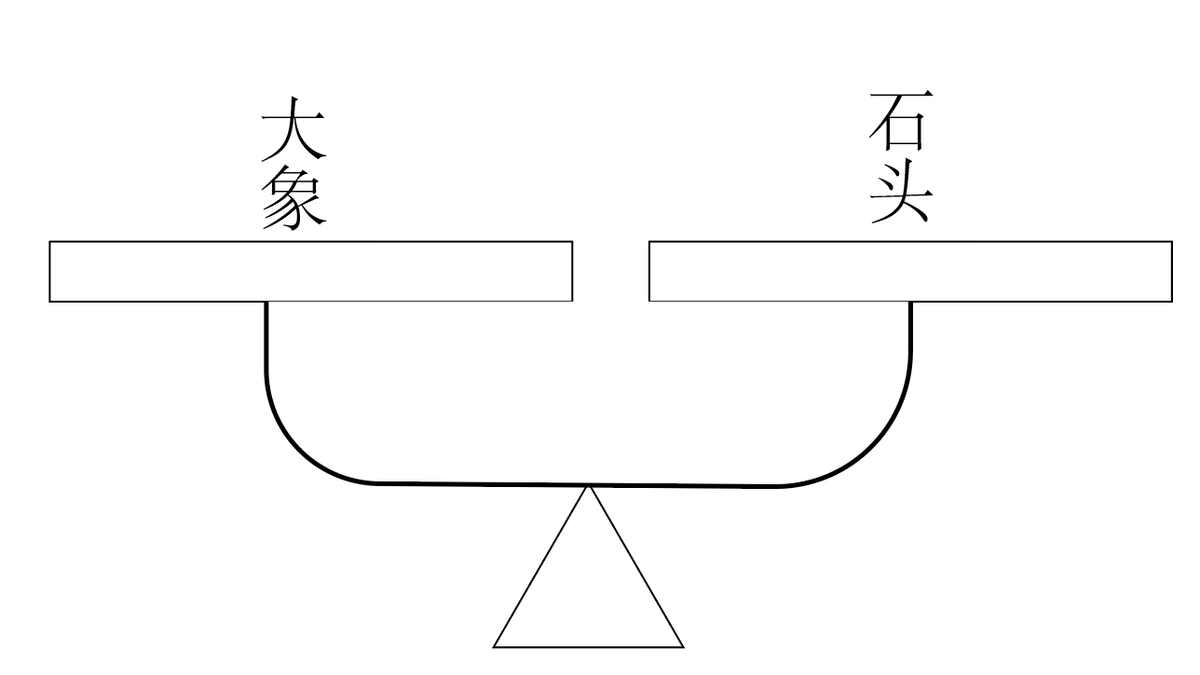
为什么称石头可以知道大象的重量。
答案是因为有船作为天平,大象在船上时下沉的深度等于石头下沉的深度,所以大象的重量=石头的重量。至此,大象的重量就称出来了。
如果孙权送给曹操的不是一头大象而是很多头大象,要知道每一头大象的体重你觉得该如何去称出一群大象的体重?要搬多少次石头?
改进的称大象方法
在把大象赶上船之前先沿着水面在船体做标记设为标记一(这里可以叫做清零)。把大象赶上船后沿着水面在船体做标记设为标记二。把大象赶下去后就得到下图船体标记线。
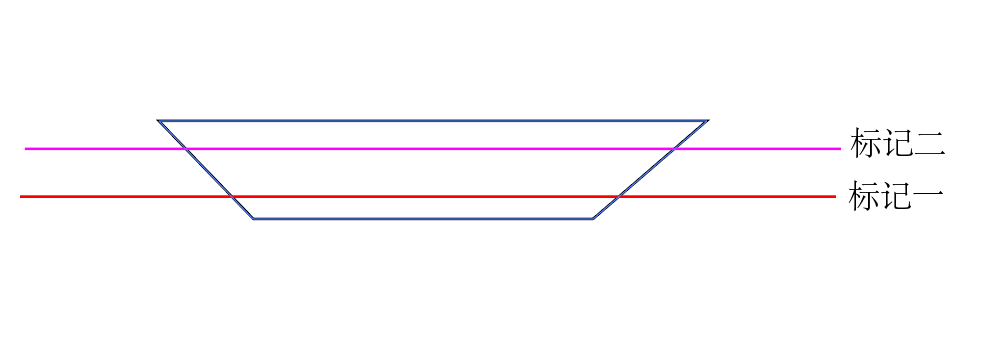
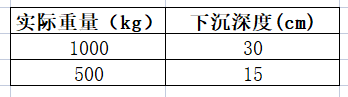
假设称完石头后石头的总重量为1000kg,用尺量出标记一到标记二的垂直高度为30cm。假设船体比较垂直的话船体的下沉深度和船上重物为线性关系,船体从标记一处开始下沉下沉深度为30cm船上的重物就是1000KG。理想状态下沉深度为15cm时船上的重物就是500KG。有如下表格数据:
以实际重量为Y轴,船体下沉深度为X轴绘制图表。设置趋势线,显示线性公式,所得线性公式为:y=33.333x。

把剩余的几头大象分别赶到船上标记船体下沉深度。根据之前计算获得的线性关系(y=33.33x,x船体下沉深度)把船体下沉深度代入线性关系即可计算出剩余几头大象的实际重量。这样的话就只需要搬一次石头即可计算出其余大象的总量。
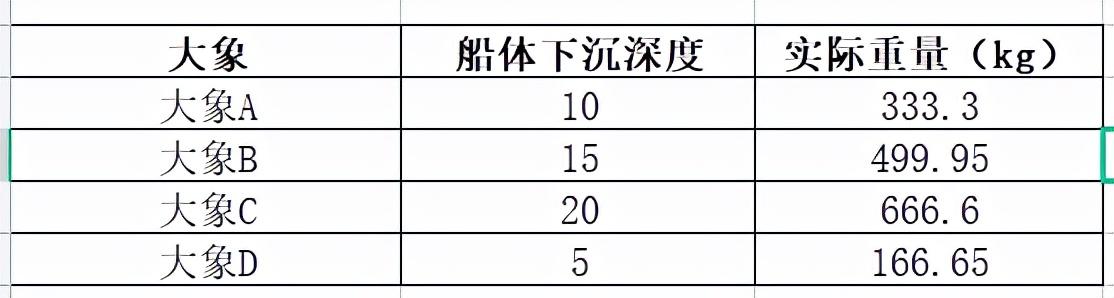
称象方法再改进
实际称象存在着较大的偏差,也没有理想的线性下沉关系。因为船体一般都是弧形的,所以下沉关系并非直线线性关系,也许是曲线。船体形状可能是这样的。
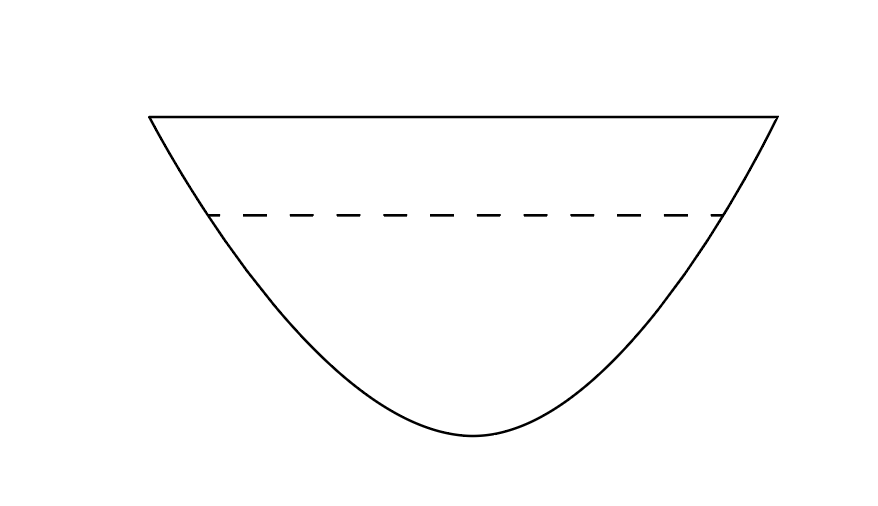
那么船体下沉的关系数据,假设。
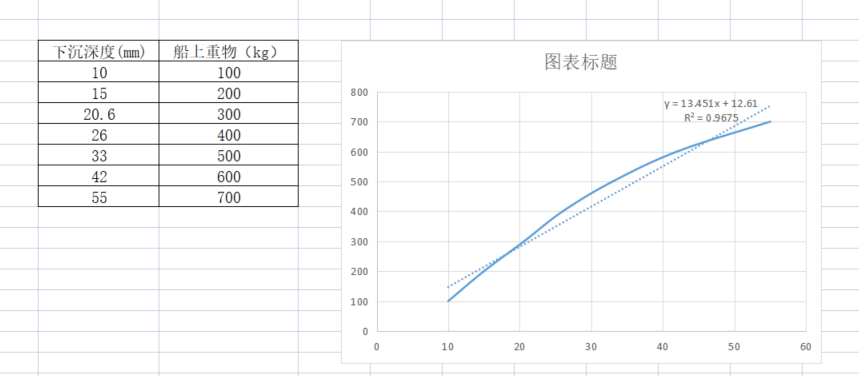
根据图表数据可知使用简单的线性关系式所计算的趋势线拟合度比较差。最终如果使用该关系式进行称象难免会存在缺斤少两的情况存在。
那如何增加准确性呢?
把线性改为多项式关系式。
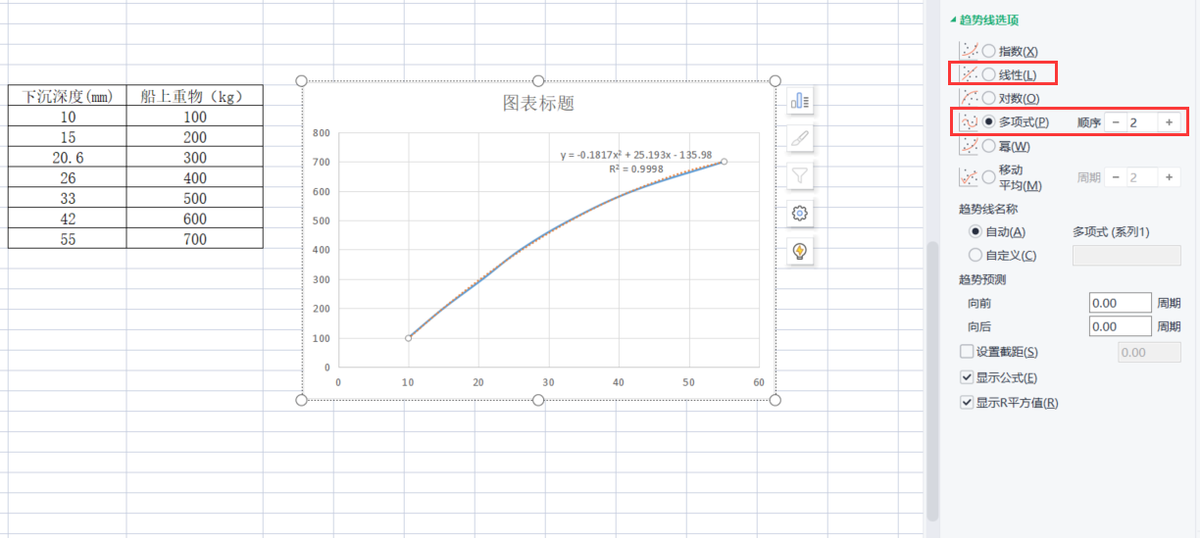
根据图中显示所知趋势线与实际几乎重合,R平方值从0.9675上升到0.9998,非常接近实际数据。
如果使用该方法称象首先用已知重量的石头按照一定比例添加到船上标记船体下沉深度记录船体下沉与重量的关系。然后计算出关系式,把大象赶到船上记录船体下沉深度,把船体下沉深度代入关系式计算出大象的重量。
思考
你知道电子秤称重的原理吗?
你知道传感器的温度补偿是什么原理吗?
你知道为什么可以通过气体压力传感器可以测量到气体的流速和容积?

